Populärteknik
Musik och matematik
Den moderna naturvetenskapen har sitt ursprung i musiken, närmare bestämt i de musikaliska experiment som den grekiske filosofen och matematikern Pythagoras utförde på 500-talet före vår tideräknings början.
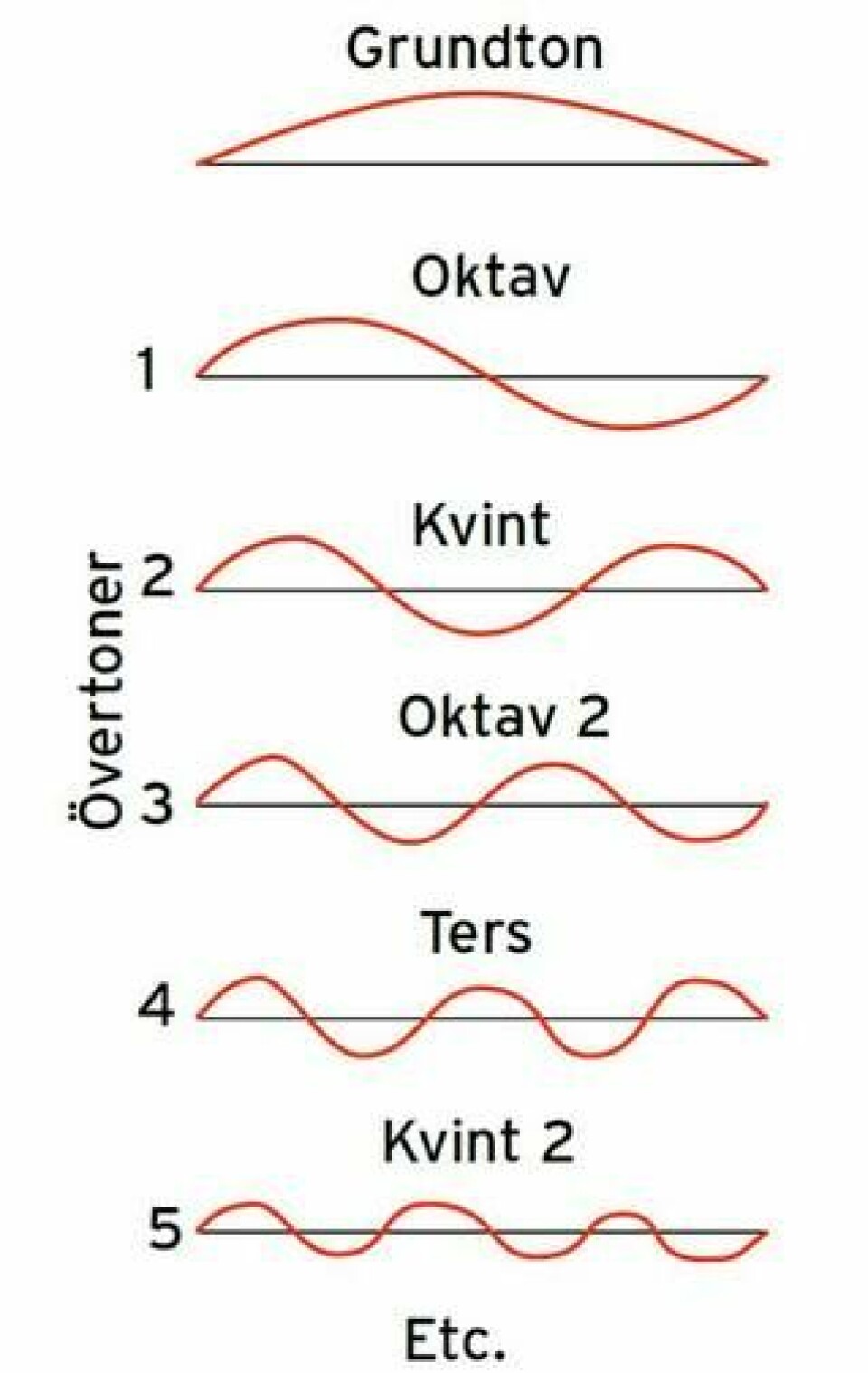
Det finns i all musik, inte bara i västerländsk, två grundläggande skönklingande tonintervall, nämligen oktaven och kvinten. Oktaven är vår tonskalas åttonde ton, den ton som låter lika som grundtonen, fast högre. Exempelvis de två första tonerna i ”Somewhere Over the Rainbow”. Kvinten är skalans femte ton. Som i början av ”Blinka lilla stjärna där”.
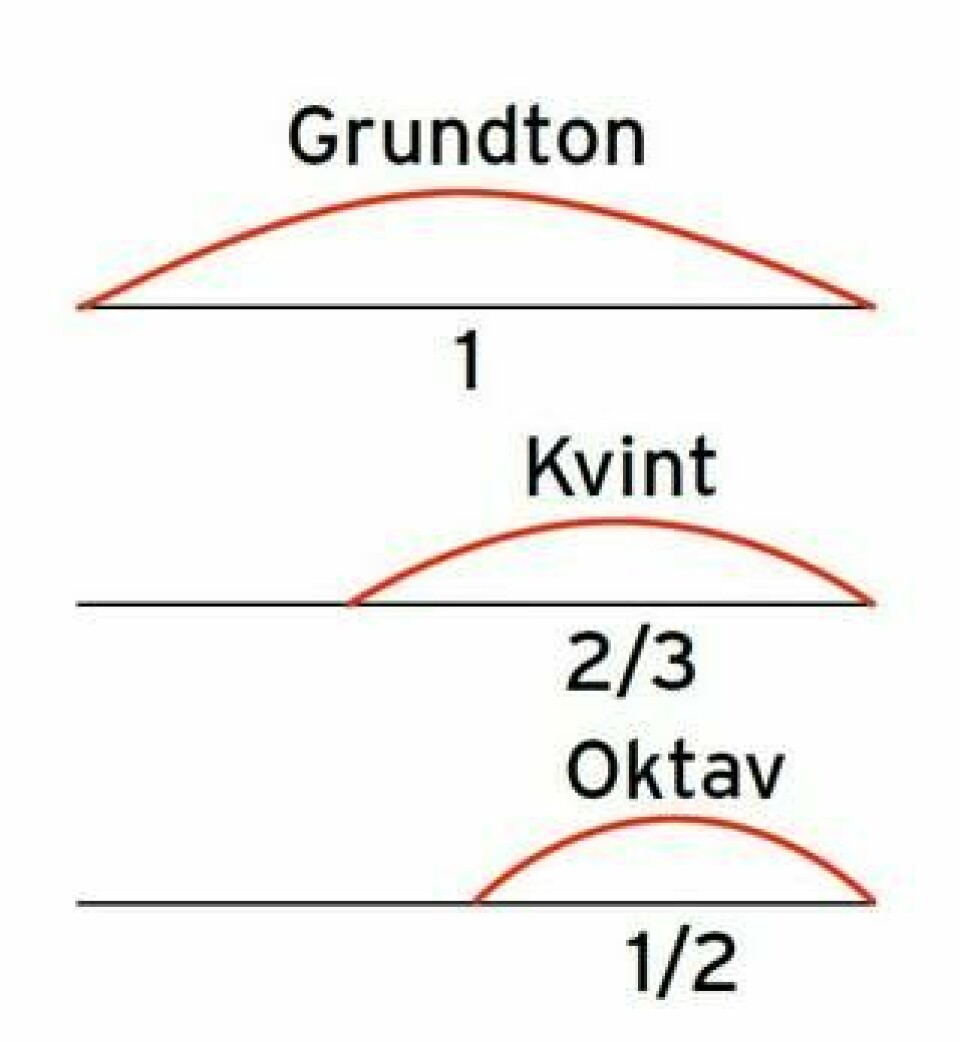
Den grekiske matematikern Pythagoras experimenterade på 500-talet före vår tideräknings början med strängar som han knäppte och slog på. Han upptäckte då att om en godtycklig sträng av en viss längd gav en viss ton – som vi kan kalla grundtonen – så gav av halva längden av samma sträng oktaven till grundtonen. Men inte nog med det. En sträng med längden 2/3 av grundtonens gav kvinten.