Populärteknik
Kan spelteorin rädda världen?
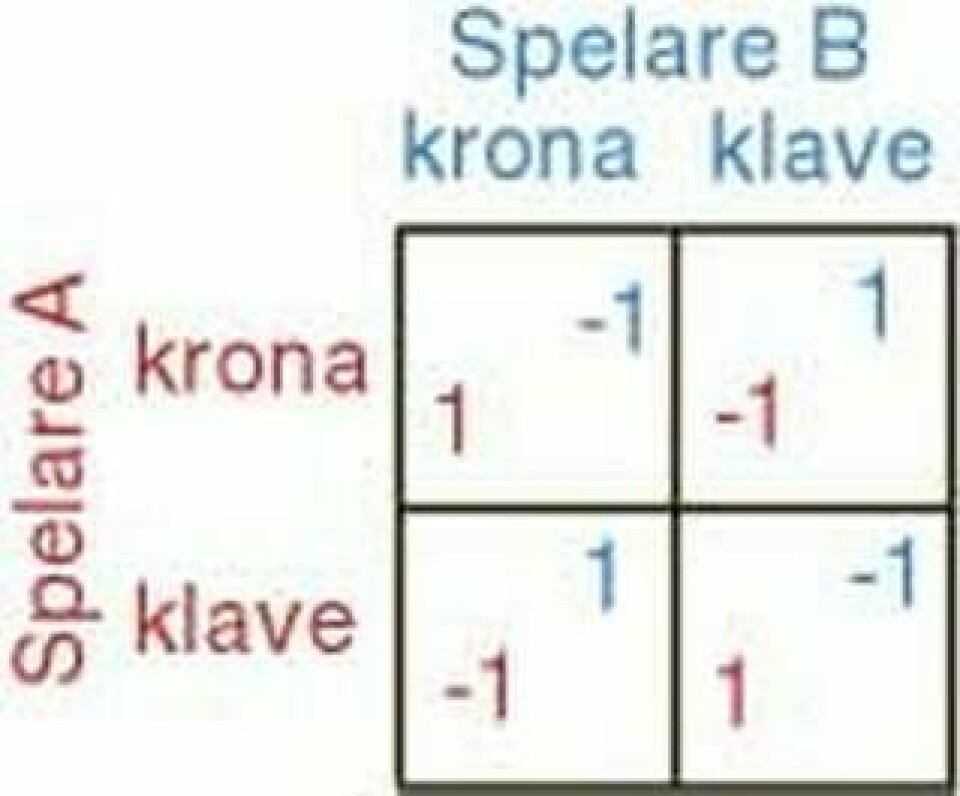
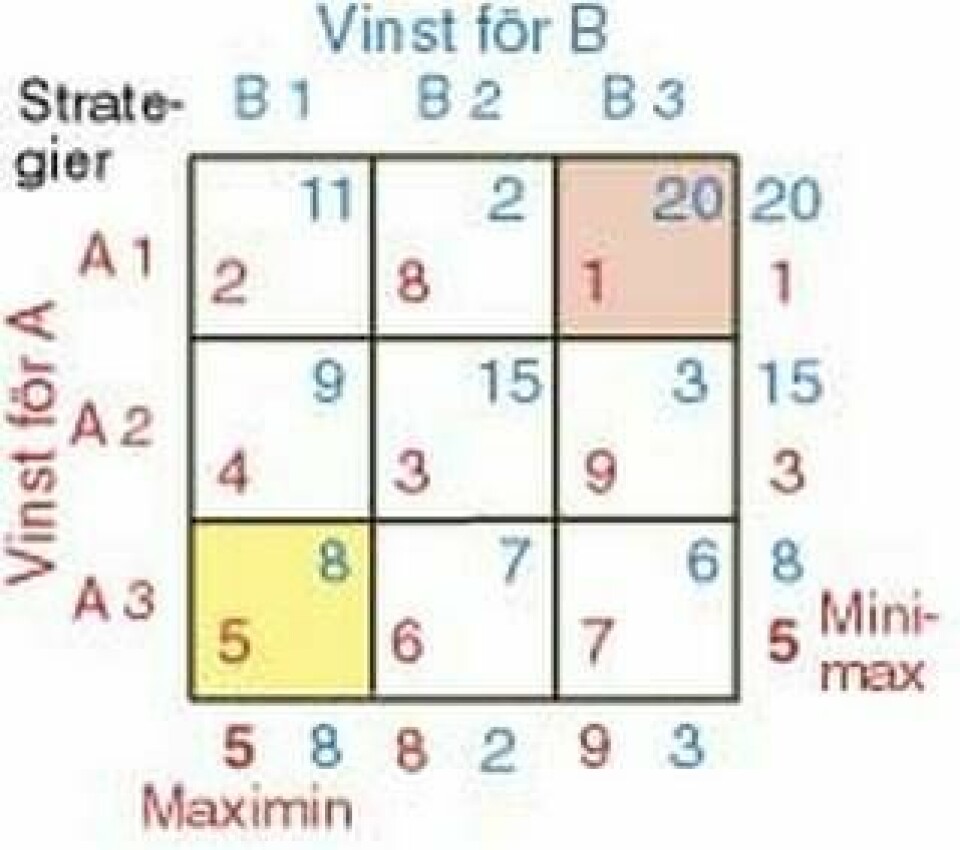
För tredje gången har ekonomipriset till Alfred Nobels minne gått till matematiker för framsteg inom spelteorin, denna gång för applikationer inom konfliktlösning. Men vad är egentligen spelteori? Är det verkligen något som kan rädda världen? Och varför är ekonomipriset så hårt kritiserat? Ny Teknik reder ut begreppen.
Annons