Populärteknik

Fraktalerna har

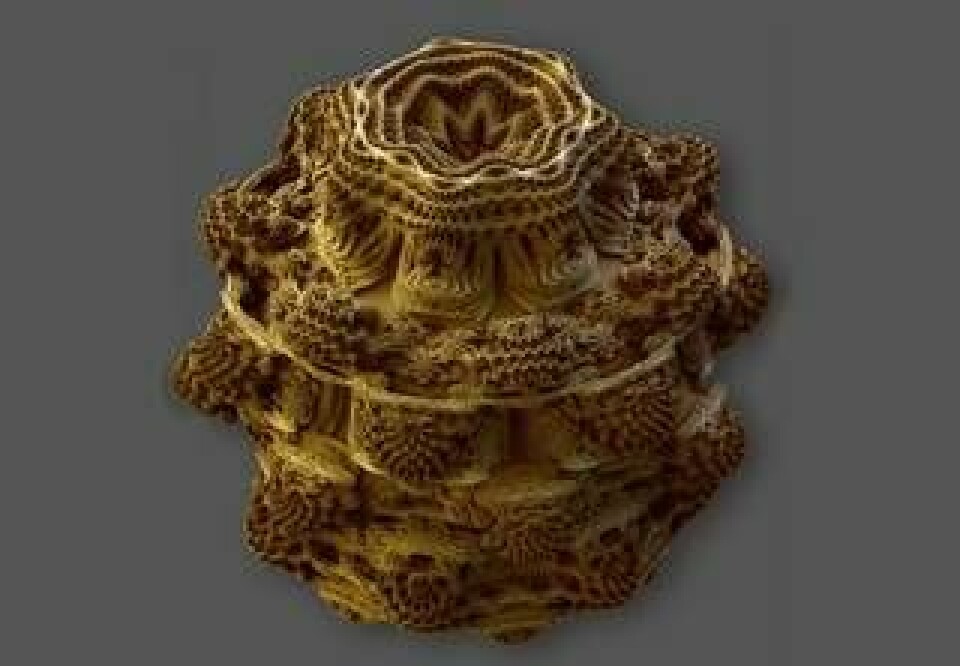
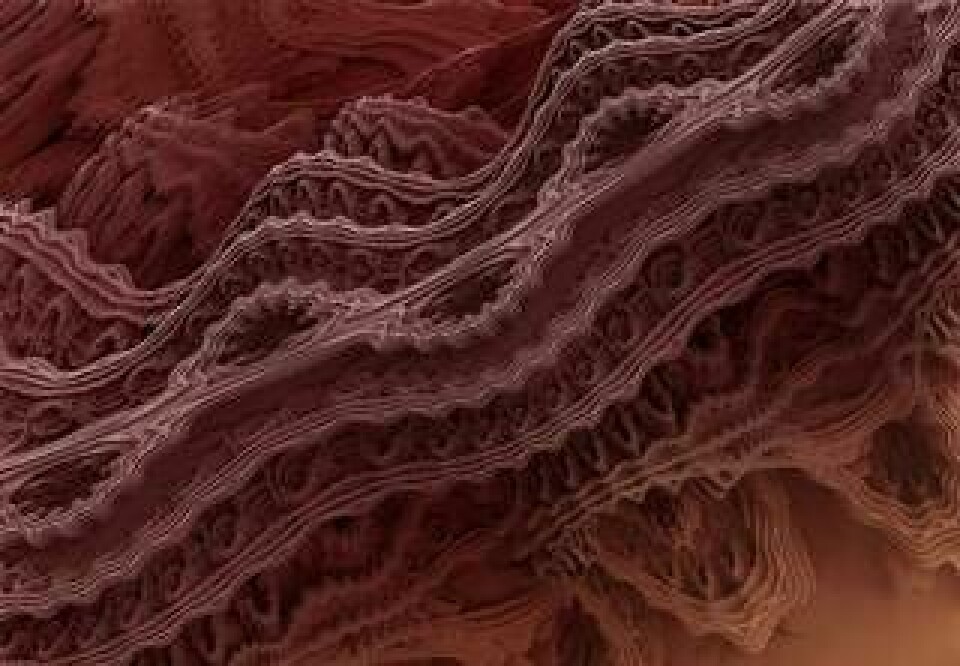
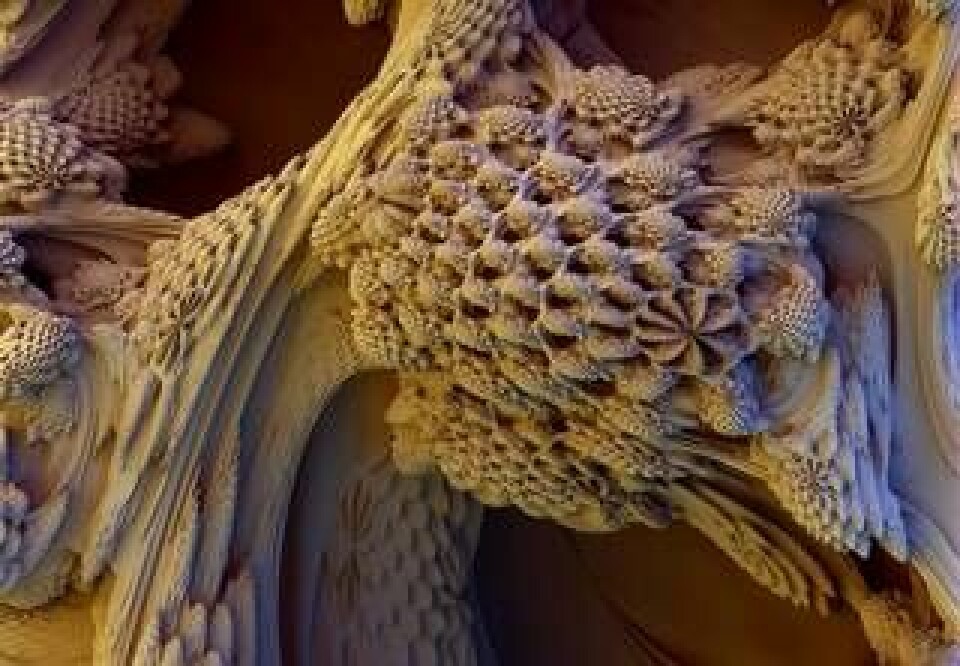
fått äkta 3D-djup

En jämförelse mellan fraktalbilder i 3D och 2D. Foto: Daniel White
Den klassiska mandelbrotbilden
Titta på ett bildspel med tio av Daniel Whites mandelbrotbilder i 3D. Foto: Daniel White
Foto: Daniel White
Foto: Daniel White
Foto: Daniel White
Foto: Daniel White
Foto: Daniel White
Foto: Daniel White
Foto: Daniel White
Foto: Daniel White
Foto: Daniel White

De klassiska mandelbrotbilderna har nu utvecklats till att bli tredimensionella. <br></br>Det är den brittiska hobbymatematikern Daniel White som hittat den matematiska formeln för 3D Mandelbrot Fractal.

Jan Melin
Jan Melin
Publicerad

I början av 1980-talet visade matematikern Benoit Mandelbrot hur man kunde skapa fantastiska bilder med hjälp av en enkel matematisk formel.

Det märkliga med dessa så kallade fraktaler var att man kunde ”zooma” in bilderna i oändlighet och för varje steg upptäcka nya formationer och mer komplexa strukturer.

Prova Ny Teknik – 149 kr
för tre månader


Tillgång till alla låsta artiklar, fördjupande kompendier,
premiumnyhetsbrev, samt e-tidningen.



Kom igång nu →

Förnyas till 299 kr/mån efter din provperiod. Ingen bindningstid. Avsluta enkelt.
Gäller endast nya prenumeranter.


Är du medlem i Sveriges Ingenjörer?

Aktivera ditt konto här

populärteknik nyheter

MEST LÄST